問題
※うまく表示されないときは、下をお試しください。
一次関数のグラフを書く
chokoan.com
解説
グラフをかく基本は、点をたくさんとって結ぶ、ということです。
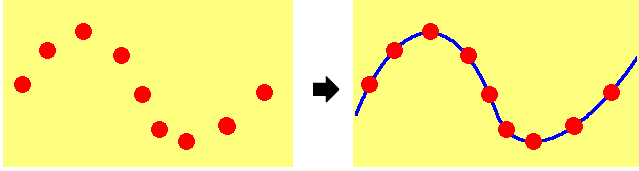
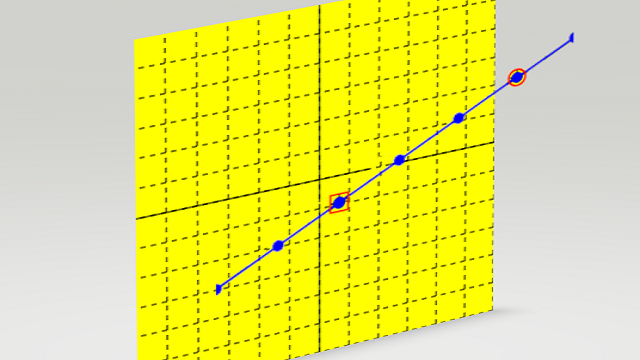
グラフの形がわかっているなら、そのぶん、点が少なくてすみます。一次関数、つまり、式が ｙ＝2ｘ＋3 みたいなときは、グラフの形が直線になることがわかっているので、たった２つの点だけでグラフがかけます。
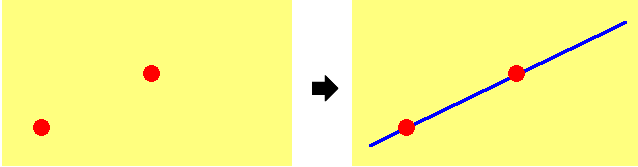
１つめの点は、とにかくガッツで見つけます。２つめの点は、変化の割合がわかっていると見つけるのがラクです。
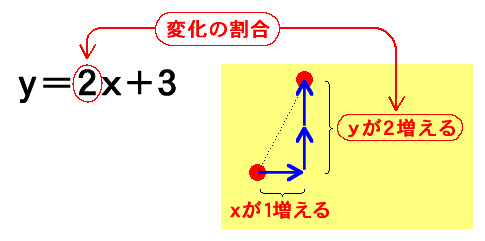
変化の割合とは、「x が 1 増えたとき、y がどれだけ増えたり減ったりするか」ということです。
（例１） ｙ＝2ｘ＋3 では、変化の割合は 2 です。なので、「x が 1 増えたとき、y が 2 増える」ことがわかります。
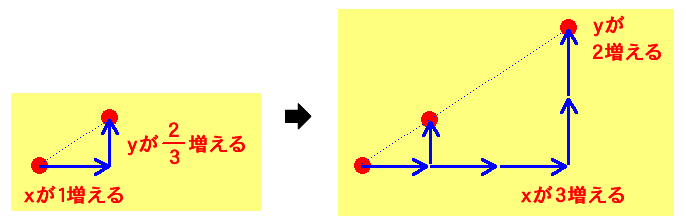
（例２） ｙ＝23 x＋4 では、変化の割合は 23 です。なので、「x が 1 増えたとき、y が 23 増える」ことがわかります。
※変化の割合が分数のときは、「 1 増える」と「 23 増える」をそれぞれ 3 倍して、「x が 3 増えたとき、y が 2 増える」と考える方がわかりやすいです。
変化の割合、と言うとなんだか難しそうですが、日常生活の身近なところにごくふつうにあります。
例えば、「1か月のお小遣いは2000円だ」というときは、1か月でお小遣いが2000円増える、ということで、1か月ごとの変化の割合は「2000円」です。
「速さが時速60km」というときは、1時間で進む距離が60km増える、ということで、1時間ごとの変化の割合は「60km」です。
（例１） ｙ＝2ｘ＋3 では、変化の割合は 2 です。なので、「x が 1 増えたとき、y が 2 増える」ことがわかります。
（例２） ｙ＝23 x＋4 では、変化の割合は 23 です。なので、「x が 1 増えたとき、y が 23 増える」ことがわかります。
※変化の割合が分数のときは、「 1 増える」と「 23 増える」をそれぞれ 3 倍して、「x が 3 増えたとき、y が 2 増える」と考える方がわかりやすいです。
変化の割合、と言うとなんだか難しそうですが、日常生活の身近なところにごくふつうにあります。
例えば、「1か月のお小遣いは2000円だ」というときは、1か月でお小遣いが2000円増える、ということで、1か月ごとの変化の割合は「2000円」です。
「速さが時速60km」というときは、1時間で進む距離が60km増える、ということで、1時間ごとの変化の割合は「60km」です。
コメント