問題
解説
※この解説では、AとBを、ある2つの数とします。最小公倍数とは
Aの倍数でもあり、Bの倍数でもある数を、AとBの公倍数といいます。
公倍数のうち、一番小さな公倍数を最小公倍数といいます。
AとBの最小公倍数の倍数は、AとBの公倍数になります。
最小公倍数の見つけ方
最小公倍数は、素因数分解をすれば、すぐに見つけることができます。
2つの数AとBをそれぞれ素因数分解したとき、次のようになったとします。(●や▲などを素因数といいます。AやBの部品のようなものです。)
A=●●▲■
B=●▲▲
このとき、AとBの最小公倍数は、
●●▲▲■
になります。
Aの部品も、Bの部品も、全部そろっているのが、最小公倍数です。
なので、Aから最小公倍数を見つけるときは、Aにどんな部品を加えると、Bの部品が全部そろうかなー?と考えます。
A●●▲■ に ▲ を加えると、
Bの部品 ●▲▲ が全部そろう。
または、Bから最小公倍数を見つけるときは、Bにどんな部品を加えると、Aの部品が全部そろうかなー?と考えます。
B●▲▲ に ●■ を加えると、
Aの部品 ●●▲■ が全部そろう。



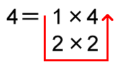
コメント